方程法是考生在行測數量關系解題常用的方法，掌握好方程法對提高做題效率很有幫助。而且列方程和解方程都有較強的技巧性。下面就列方程的原則進行梳理。

　　原則一：優先設題目中所求的量為未知數，也就是問啥設啥.

　　【例1】某零件加工廠按照工人完成的合格零件和不合格零件數支付工資，工人每做出一個合格零件能得到工資10元，每做出一個不合格的零件將被扣除5元。已知某人一天共做了12個零件，得到工資90元，那么他在這一天做了多少個不合格零件?( )

　　A.2 B.3

　　C.4 D.6

　　【答案】D

　　【解析】設不合格個數為X，則合格個數12-X，根據題意，10(12-X)-5X=90，解得X=2。因此，答案選擇C選項。

　　【例2】某產品售價為67.1元，在采用最新技術生產節約10%成本之后，售價不變，利潤可比原來翻一番。問該產品最初的成本為多少元?

　　A.51.2 B.54.9

　　C.61 D.62.5

　　【答案】C

　　【解析】設產品最初的成本為X，則采用最新技術生產節約后成本成本為0.9X，根據題意，2(67.1-X)=67.1-0.9X，解得X=61。因此，答案選擇C選項。

　　原則二：方便方程解決，未知數數設核心變量

　　很多題目問什么設什么時候不便于直接尋找等量關系，可將便于尋找等量關系的核心變量量設為未知數。

　　【例3】小王周末組織朋友自助游，費用均攤，結帳時，如果每人付450元，則多出100元;如果小王的友每人付430元，小王自己要多付60元才剛好，這次活動人均費用是：

　　A.437.5元 B.438.0元

　　C.432.5元 D.435.0元

　　【答案】A

　　【解析】設活動人數有X人，根據題意450X-100=430X+60，解得X=8。因此有8人，人均費用為(430×8+60)÷8=437.5，答案選擇A選項。原則三：根據比例份數設未知數

　　【例4】某有色金屬公司四種主要有色金屬總產量的1/5為鋁，1/3為銅，鎳的產量是銅和鋁產量之和的1/4，而鉛的產量比鋁多600噸，問該公司鎳的產量為多少噸?

　　A.600 B.800

　　C.1000 D.1200

　　【答案】A

　　【解析】根據“有色金屬總產量的1/5為鋁，1/3為銅”，可以設有色金屬總產量為15X，則鎳的產量為2X,根據題意15X=3X+5X+2X+3X+600，解得2X=600，因此，答案選擇B選項。

　　【例5】某俱樂部中女會員的人數比男會員的一半少61人，男會員的人數比女會員的3倍多2人，問該俱樂部共有會員多少人?( )

　　A.475人 B.478人

　　C.480人 D.482人

　　【答案】D

　　【解析】題干中有“男會員的一半”，可設男會員人數=2X，則女會員人數=X-61，根據題意，2X=3×(X-61)+2，解得X=181，總人數=3X-61=482。因此，答案選擇D選項。

　　原則四：題干復雜時，借助列表法找等量關系

　　【例6】甲乙丙三人在2008年的年齡(周歲)之和為60，2010年甲是丙年齡的兩倍，2011年乙是丙年齡的兩倍，問甲是哪一年出生的?( )

　　A.1988 B.1986

　　C.1984 D.1982

　　【答案】C

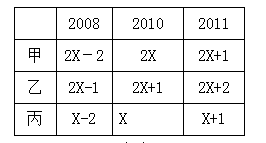
　　【解析】設2010年丙的年齡為X，根據題意如下表

　　根據2X-2+2X-1+X-2=60，解得X=13，甲2010年的年齡=2X=26，出生于1984年。因此，答案選擇C選項。

　　【例7】某公司甲、乙兩個營業部共有50人，其中32人為男性。已知甲營業部的男女比例為5∶3，乙營業部的男女比例為2∶1，問甲營業部有多少名女職員?( )

　　A.18 B.16

　　C.12 D.9

　　【答案】C

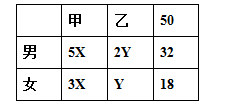
　　【解析】設甲營業部女生為3X,乙營業部女生為Y,根據題意如下表

　　根據5X+2Y=32，3X+Y=18，解得X=4，因此甲營業部女生為12人，答案選擇C。

　　公務員考試時間急迫，爭分奪秒，掌握列方程原則，有助于順利解答數量關系題目。以此在以后復習需要多加練習，領會其中的技巧，提高解題速度。

關注"566公務員"官方微信，獲取真題及答案、最新資訊等信息!

公務員考試題庫【手機題庫下載】丨微信搜索"566公務員"

　　相關推薦：

　　考試吧整理：各地2016公務員考試報名時間匯總

　　考試吧整理：各地2016公務員考試報名入口匯總

　　考試吧整理：各地2016年公務員考試準考證打印入口匯總