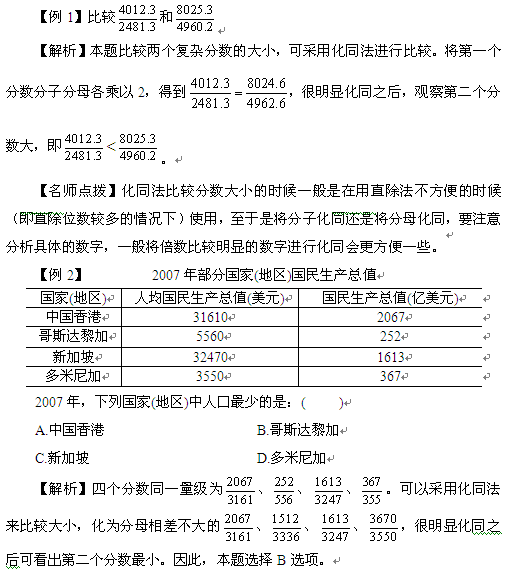
在資料分析考試當中，經常會出現兩個復雜分數的大小比較，為了比較方便，常常運用“化同法”。所謂“化同法”，是指“在比較兩個分數大小時，將這兩個分數的分子或分母化為相同或相近，從而達到簡化計算”的速算方式。“化同法”一般包括三種形式：將分子(或分母)化為完全相同，從而只需要再看分母(或分子)即可;將分子(或分母)化為相近之后，出現"某一個分數的分母較大而分子較小"或"某一個分數的分母較小而分子較大"的情況，則可直接判斷兩個分數的大小;將分子(或分母)化為非常接近之后，再利用其它速算技巧進行簡單判定。

　　事實上在資料分析考查題目當中，將分子(或分母)化為完全相同一般是不可能達到的，所以化同法更多的是“化為相近”而非“化為相同”。

　　【名師點撥】分數比較大小的首要問題是分析各個分數是否量級相同，量級相同的情況下可以采用化同法將分母或者分子化為相近的數，分子或分母一旦有一個接近時，比較大小就變得非常直觀了。

　　化同法在資料分析考試當中使用頻率并不是太高，遠遠沒有估算法、直除法那么普遍。但是考生可以將化同法作為補充的速算技巧來掌握，對于部分分數比較類題目使用化同法還是非常方便的。

　　相關推薦：

　　2014年內蒙古公務員行測數量關系：整除思想

　　2014內蒙古公務員行測言語理解：備考誤區探析

　　2014內蒙古公務員數量關系：數學運算快速解題