
⒈模式圖和藥-時關系表達式口服、肌肉或皮下注射用藥時,和前面討論的血管內給藥不同。此時即存在藥物從用藥部位吸收進入血液的過程,也存在藥物自體內(血液)消除的影響。由于絕大多數藥物均是以被動轉運的方式吸收,故上述兩個過程都按一級動力學方式進行。其模式圖如下(圖9-6):
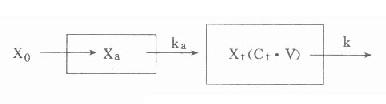
Xa:t時吸收部位藥量
Ka:吸收速率常數其它參數同圖9-3
圖9-6 血管外用藥模式圖
根據上述關系及模式圖,可建立如下微分方程組:
dxa/dt=-Ka·Xa(吸收部位藥物衰減速率)
dxa/dt=-Ka·Xa--K·X(血液等藥物分布室內藥物衰減速率)
解此微分方程組得
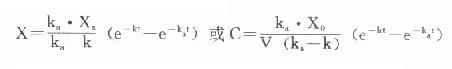
若考慮口服時吸收不完全而引入吸收分數F,則:

式⒀即為單劑血管外用藥時,血管濃度隨時間變化的基本表達式。
⒉藥動學參數及計算通過血管外用藥計算藥動學參數多用殘數法(methodofresidual)。該法基本指導思想是,以血管外用藥能獲治作用的藥物,必然Ka>>k,才有可能在體內達到治療血藥濃度,因此,當t足夠大時,首先e-kat→0此時式⒀可寫作:
C=A·e-kt取對數得lgC=lgA-kt/2.303
也就是說單劑血管外用藥時,經過一段時間后,其血藥濃度的變化可視做只受消除的影響,即進入消除相(圖9-7)。
此時按前面介紹的單劑靜脈注射藥動學參數計算法,可求得A、k和消除t1/2。而在進入消除相以前的時間內,血藥濃度為吸收和消除兩因素共同作用的結果。若將式⒀展開移項則得
A·e-kt-C=A·e-kat,令Cr=A·e-kt-C,
Cr為消除相外推段某時點血藥濃度減去該時點實測濃度的殘數或差值(注意不是對數值相減)。則:
Cr=A·e-kat,取對數得TgCr=IgA-kat/2.303
此即分布相藥-時關系的表達式(圖9-6),同理可求算得ka和吸收t1/2。
在計算其它藥動學參數時,反映藥物被機體吸收利用程度的吸收分數F,即生物利用度(bioavailability)是必須首先先知道的。血管外注射用藥時,一般均視為F=1。而現在多數口服藥在說明書中已告知F值,否則需根據某藥口服時AUC與該藥同劑量靜脈注射時的AUC相比計算出。口服時的AUC可用前述梯形法,或按下列積分法公式求得:
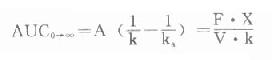
其他藥動學參數計算見下。
⑴表觀分布容積:
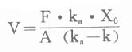
⑵清除率:Cl=k·V
⑶達峰時間(timeofthepeakconcentration,tp):即血管外給藥時,達到最高濃度所需時間。由于在此時,血藥濃度變化速率dC/dt=0,故可推導出:
⑷峰濃度(maximumconcentration,Cmax):將tp代入式⒀可得:

| 北京 | 天津 | 上海 | 江蘇 | 山東 |
| 安徽 | 浙江 | 江西 | 福建 | 深圳 |
| 廣東 | 河北 | 湖南 | 廣西 | 河南 |
| 海南 | 湖北 | 四川 | 重慶 | 云南 |
| 貴州 | 西藏 | 新疆 | 陜西 | 山西 |
| 寧夏 | 甘肅 | 青海 | 遼寧 | 吉林 |
| 黑龍江 | 內蒙古 |