在近期的廣東省考中，12、13年連續兩年出現了邊端計數問題。其中12年考察的是方陣問題，且對方陣問題的知識點考察的較為全面。

　　那么關于方陣問題，具體有哪些知識點可能會被考察呢?主要有兩類：方陣總人數和方陣中各圈人數。下面我們先對知識點進行講解。

　　首先，我們來看兩個方陣：(每個點代表一個人)

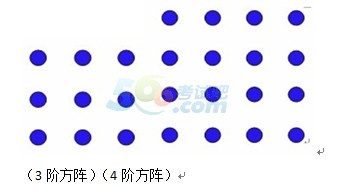
　　左邊的有3行3列，稱為3階方陣;右邊的有4行4列，稱為4階方陣。相似地，當方陣有N行N列時，稱為N階方陣。

　　那么方陣中總人數如何計算呢?我們看到，3階方陣中每行有3人，共有3行，則共有3×3=9人;4階方陣中每行有4人，共有4行，則共有4×4=16人。以此類推，N階方陣則有N×N人，這也就是我們方陣總人數的計算公式：

　　N階方陣總人數=N×N

　　那么第二個知識點，方陣中各圈人數如何計算呢?我們以4階方陣為例：

　　如圖，將其最外圈分為4部分計算，每部分3人，則其最外圈共有3×4=12人。相似地，對于N階方陣，沿其四條邊將其分為4個部分，每部分N-1人，則共有4×(N-1)=4N-4人。這也就是我們方陣最外圈人數的計算公式：

　　N階方陣最外圈人數=4N-4

　　那么方陣中其它圈的人數如何計算呢?我們發現要算一個方陣第二圈的人數，只要將最外圈的人剔除，將原N階方陣變為一個N-2階方陣，再計算這個N-2階方陣最外圈人數即可。那么第二圈人數即為4×(N-2-1)=4N-12人。比其相鄰靠外一圈的人數少了8人。所以我們推出定理：

　　方陣中相鄰兩圈人數相差8人

　　以上三點，也就是我們公考行測中可能會遇到的關于方陣問題的知識點，希望考生牢記，不需要在考試時現算現推，而直接代入使用，節省時間。

　　下面我們用一道真題看看這些理論如何付諸實踐。

　　(廣東2012-49)有綠、白兩種顏色且尺寸相同的正方形瓷磚共400塊。將這些瓷磚鋪在一塊正方形的地面上：最外面的一周用綠色瓷磚鋪，從外往里數的第二周用白色的瓷磚鋪，第三周用綠色瓷磚，第四周用白色瓷磚……這樣依次交替鋪下去，恰好將所有瓷磚用完。這塊正方形地面上的綠色瓷磚共有()塊。

　　A. 180

　　B. 196

　　C. 210

　　D. 220

　　題干中給出瓷磚總數為400，且鋪在正方形地面上，則可通過N階方陣總數公式：總數=N×N計算出這些瓷磚鋪成一個20階方陣。而最外圈為綠色，瓷磚數為4N-4=4×20-4=76塊，而相鄰兩圈相差8塊，則中間相隔一圈的兩圈瓷磚間相差16塊。即各圈綠色瓷磚間相差16塊。通過枚舉法，可以逐一減出綠色瓷磚圈的瓷磚塊數分別為：76，60，44，28，12。再減16為負數，則12塊為最內一圈綠色瓷磚的塊數。發現這是一個等差數列，用總數=中位數×個數計算綠色磚總數=44×5=220塊。因此答案為D選項。

　　可以想象，如果之前不知道關于方陣問題的幾個定理，在考試中現推、現算，這道題將花費大量的時間。而直接使用公式代入計算，將節省大量畫圖、推導過程，簡潔明了。

　　相關推薦：

　　2014年廣東公務員行測："多集合反向構造"不復雜

　　2014廣東公務員考試數量關系:"工程問題"很簡單

　　2014年廣東公務員行測備考：最值問題備考技巧