>>>2018年中級會計職稱《財務管理》預習知識點匯總

　　貨幣時間價值的計算

　　(一)利息的兩種計算方法

　　單利計息：只對本金計算利息，各期利息相等。

　　復利計息：既對本金計算利息，也對前期的利息計算利息，各期利息不同。

　　(二)復利終值與現值的計算

　　終值(Future Value)是現在的一筆錢或一系列支付款項按給定的利息率計算所得到的在某個未來時間點的價值。

　　現值(Present Value)是未來的一筆錢或一系列支付款項按給定的利息率計算所得到的現在的價值。

　　【教材例2-1】某人將100元存入銀行，復利年利率2%，求5年后的終值。

　　復利終值的計算公式

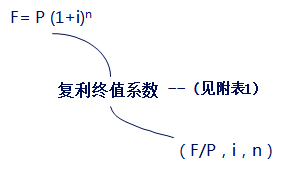
　　復利終值系數表

　　1元的復利終值系數，利率I,期數 n 即(F/P,i,n)。

　　【教材例2-1解答】

　　F=P(1+i)n

　　=100×(l+2%)5=110.41 (元)

　　或：

　　F=P×(F/P,i,n)

　　=100×(F/P,2%,5)

　　=100×1.1041=110.41 (元)

　　2、復利現值

　　復利現值計算公式：

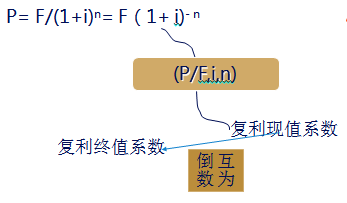
　　【教材例2-2】某人為了5年后能從銀行取出100元，在復利年利率2%的情況下，求當前應存入金額。

　　復利現值系數表

　　期數為n的復利現值系數(P/F,i,n )

　　【解答】

　　P=F/(1 +i)n

　　=100/(1 +2% )5=90. 57 (元)

　　或：

　　P=F×(P/F,i,n)

　　=100×(P/F,2%,5)

　　=100×0.9057=90.57

　　【例題·計算題】某人擬購房，開發商提出兩種方案，一是現在一次性付80萬元，另一方案是5年后付100萬元若目前的銀行存款利率是7%，應如何付款?

　　復利終值系數表

　　1元的復利終值系數，利率I,期數 n 即(F/P,i,n).

　　復利現值系數表

　　期數為n的復利現值系數( P/F,i,n )

　　【例題答案】

　　(1)用終值比較：

　　方案一的終值：F =800000×(1+7%)5=1122080

　　或 F =800000 ×(F/P，7%，5)=800000×1.4026=1122080

　　方案二的終值：F=1000000

　　所以應選擇方案二。

　　(2)用現值比較

　　方案二的現值：P = 1000000×(1+ 7%)-5

　　或P=1000000×(P/F，7%,5 )=1000000×(0.713)

　　=713000<800000

　　解答：按現值比較，仍是方案2較好

　　結論：

　　(1)復利的終值和現值互為逆運算。

　　(2)復利的終值系數(1+i)n和復利的現值系數1/(1+i)n互為倒數。

掃描/長按二維碼幫助會計師考試通關

2017中級會計成績查詢

2018初級會計報名時間

下載歷年會計師真題卷

了解2018會計報考指南

會計職稱萬題庫下載 | 微信搜索"萬題庫會計職稱考試"

　　相關推薦：

　　2018年中級會計師考試應該何時開始復習

　　各地2017年中級會計職稱成績查詢時間匯總

　　考試吧中級會計職稱考試各科目每日一練匯總

　　2018年中級會計職稱各階段考試真復習計劃匯總