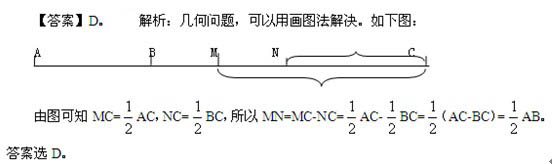
近兩年多省同天考試行測科目數量關系部分考點分布較為穩定，重點是對數學運算的考查，主要有以下12種題型：計算問題、和差倍比問題、行程問題、工程問題、利潤問題、統計問題、幾何問題、推理問題、容斥問題、盈虧問題、年齡問題、時鐘問題。專家在此針對以上考點現總結五種基本方法如下：

　　一、特值法

　　當題目中未給出具體的量或某個量、某些量的數據值對計算結果不會產生任何影響時可用特值法，將特指設為1或設為最小公倍數或設為其他數值，此時要分情況而定，常用于行程、工程、利潤等問題。

　　【例題1】某公司三名銷售人員2011年的銷售業績如下：甲的銷售額是乙和丙銷售額的1.5倍，甲和乙的銷售額是丙的銷售額的5倍，已知乙的銷售額是56萬元，問甲的銷售額是：

　　A.144萬元 B.140萬元

　　C.112萬元 D.98萬元

　　【答案】A。解析：甲∶(乙+丙)=3∶2，總銷售額為5的倍數;(甲+乙)∶丙=5∶1，總銷售額為6的倍數。設總銷售額為30份，甲占30÷(3+2)×3=18份，丙占30÷(5+1)=5份，乙占30-18-5=7份。乙銷售額為56萬，每份是56÷7=8萬。所以甲銷售額為8×18=144萬。

　　二、方程法

　　方程法是指將題目中未知的數用變量(如x，y)表示，根據題目中所含的等量關系，列出含有未知數的等式(組)，通過求解未知數的數值來解應用題的方法。

　　方程法應用范圍較為廣泛，省考數學運算絕大部分題目，如行程問題、工程問題、盈虧問題、和差倍比問題、濃度問題、利潤問題、年齡問題等均可以通過方程法來求解。

　　【例題2】甲工人每小時可加工A零件3個或B零件6個，乙工人每小時可加工A零件2個或B零件7個。甲、乙兩工人一天8小時共加工零件59個，甲、乙加工A零件分別用時為x小時、y小時，且x、y皆為整數，兩名工人一天加工的零件總數相差：

　　A.7個 B.6個 C.5個 D.4個

　　【答案】C。解析：甲加工了3x+6(8-x)=48-3x;乙加工了2y+7(8-y)=56-5y。故48-3x+56-5y=59，整理得3x+5y=45。5y與45均是5的倍數，3x也是5的倍數，因此x是5的倍數。x是小于等于8的正整數，所以x只能取5，此時y=6。甲加工了48-3×5=33個零件，乙加工了59-33=26個零件，兩者相差33-26=7個零件。

　　三、圖解法

　　圖解法是指利用圖形來解決數學運算的方法。圖解法簡單直觀，能夠清楚表現出問題的變化過程，但是容易出錯，在畫圖形的時候一定要保證圖形和數字保持一一對應的關系。常用的幾何模型有線段圖(表示量與量關系)、文氏圖(集合之間關系)、直角坐標系等。

　　一般來說，圖解法適用于絕大部分題型，尤其是在行程問題、年齡問題、容斥問題等強調分析過程的題型中應用得很廣。

　　【例題3】一條路上依次有A、B、C三個站點，加油站M恰好位于AC的中點，加油站N恰好位于BC的中點。若想知道M和N兩個加油站之間的距離，只需要知道哪兩點之間的距離?

　　A.CN B.BC C.AM D.AB