

【知識點2】公司資本成本計算
一、普通股資本成本
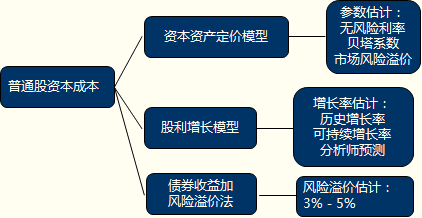
1.資本資產定價模型
| 模型 | 資本資產定價模型:Ks=RF+β×(Rm-RF) | |
| 參數確定 | RF | 長期政府債券的到期收益率(一般使用名義利率) |
| β | (1)定義法 (2)回歸分析法 【提示】①選擇預測期間長度時注意公司風險特征變化; ②收益計量間隔一般為月或周。 | |
| Rm | 歷史數據分析:①長期;②一般幾何平均數 【提示】注意算術平均數與幾何平均數的計算原理。 | |
【提示】
【例·計算題】某證券市場最近兩年的相關數據見下表。
| 時間(年末) | 價格指數 | 市場收益率 |
| 0 | 2 500 | |
| 1 | 4 000 | (4 000-2 500)/2 500=60% |
| 2 | 3 000 | (3 000-4 000)/4 000=-25% |
要求:計算平均算術平均收益率和幾何平均收益率
『正確答案』
算術平均收益率=[60%+(-25%)]/2=17.5%
【例·單選題】(2010考題)下列關于“運用資本資產定價模型估計權益成本”的表述中,錯誤的是( )。
A.通貨膨脹率較低時,可選擇上市交易的政府長期債券的到期收益率作為無風險利率
B.公司三年前發行了較大規模的公司債券,估計β系數時應使用發行債券日之后的交易數據計算
C.金融危機導致過去兩年證券市場蕭條,估計市場風險溢價時應剔除這兩年的數據
D.為了更好地預測長期平均風險溢價,估計市場風險溢價時應使用權益市場的幾何平均收益率
『正確答案』C
『答案解析』估計市場風險溢價時,為了使得數據計算更有代表性,應該選擇較長的時間跨度,其中既包括經濟繁榮時期,也包括經濟衰退時期。
2.股利增長模型
| 模型 | Ks=D1/P0+g 若考慮發行成本,新發股票成本=D1/P0(1-f)+g | |
| 參數確定(g) | 歷史增長率 | ①按幾何平均數計算增長率;②按算術平均數計算增長率 【提示】一般采用幾何平均數 |
| 可持續增長率 | ||
| 證券分析師預測 | 不穩定增長率平均化(幾何平均增長率) 【提示】計算資本成本時,注意D1的問題。 | |
【例】ABC公司2001年-2005年的股利支付情況見表。
| 年份 | 2001 | 2002 | 2003 | 2004 | 2005 |
| 股利 | 0.16 | 0.19 | 0.20 | 0.22 | 0.25 |
『正確答案』
ABC公司的股利(算術)增長率為:
g=[(0.19-0.16)/0.16+(0.20-0.19)/0.19+(0.22-0.20)/0.20+(0.25-0.22)/0.22]×100%/4=11.91%
【例·計算題】A公司的當前股利為2元/股,股票的實際價格為23元。證券分析師預測,未來第1年的股利增長率為9%,以后每年下降1個百分點,至第5年下降為5%,并一直保持下去。
要求:
(1)根據分析師的預測,計算未來第30年的股利;
(2)根據未來30年的預計股利,計算股利的幾何平均增長率;
(3)假設A公司按照幾何平均增長率固定增長,計算A公司的股權成本。
『正確答案』(1)未來5年的增長率及股利計算如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | |
| 增長率 | 9% | 8% | 7% | 6% | 5% | |
| 股利(元/股) | 2 | 2.1800 | 2.3544 | 2.5192 | 2.6704 | 2.8039 |
未來第30年的股利=2.8039×(1+5%)25=9.4950
(2)設平均增長率為g:
2×(1+g)30=9.4950
g=5.3293%
(3)
Ks=2×(1+5.3293%)/23+5.3293%=14.49%
3.債券收益加風險溢價法
| 模型 | Ks=Kdt(稅后債務成本)+RPc | |
| 參數確定 | 經驗估計 | 一般認為,某企業普通股風險溢價對其自己發行的債券來講,大約在3%~5%之間。對風險較高的股票用5%,風險較低的股票用3%。 |
| 歷史數據分析 | 比較過去不同年份的權益收益率和債務收益率。 | |
| 北京 | 天津 | 上海 | 江蘇 | 山東 |
| 安徽 | 浙江 | 江西 | 福建 | 深圳 |
| 廣東 | 河北 | 湖南 | 廣西 | 河南 |
| 海南 | 湖北 | 四川 | 重慶 | 云南 |
| 貴州 | 西藏 | 新疆 | 陜西 | 山西 |
| 寧夏 | 甘肅 | 青海 | 遼寧 | 吉林 |
| 黑龍江 | 內蒙古 |